基于信息熵进行划分选择的决策树算法

任务

试用python编程实现基于信息熵进行划分选择的决策树算法，并为P84页表4.3 中去掉“含糖率属性和编号为17的西瓜” 以后的数据生成一棵决策树。

算法原理

1.信息熵

“信息熵”(information entropy)是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第k类样本所占的比例为 $ p_ {k} $ (k=1,2, $ \cdots $ ,|y|),则D的信息熵定义为

Ent(D)的值越小,则D的纯度越高。

2.信息增益

假定离散属性a有V个可能的取值{ $ a^ {1} $ , $ a^ {2} $ , $ \cdots $ , $ a^ {V} $ },若使用a来对样本集D进行划分,则会产生V个分支结点,其中第v个分支结点包含了D中所有在属性a上取值为 $ a^ {v} $ 的样本,记为 $ D^ {v} $ .我们可根据信息熵定义计算出 $ D^ {v} $ 的信息熵，再考虑到不同的分支结点所包含的样本数不同, 给分支结点赋予权重 $ |D^ {v}|/|D|$,
即样本数越多的分支结点的影响越大,于是可计算出用属性a对样本集D进行划分所获得的“信息增益”(information gain)

一般而言，信息增益越大，则意味着使用属性 来进行划分所获得的“纯度提升”越大。我们所以要做的就是不断地从当前剩余的属性当中选取最佳属性对样本集进行划分。信息增益对可取值数目较多的属性有所偏好。

算法伪代码

image-20220321200618126

数据集

编号 色泽 根蒂 敲声 纹理 脐部 触感 密度 好瓜
1 青绿 蜷缩 浊响 清晰 凹陷 硬滑 0.697 是
2 乌黑 蜷缩 沉闷 清晰 凹陷 硬滑 0.774 是
3 乌黑 蜷缩 浊响 清晰 凹陷 硬滑 0.634 是
4 青绿 蜷缩 沉闷 清晰 凹陷 硬滑 0.608 是
5 浅白 蜷缩 浊响 清晰 凹陷 硬滑 0.556 是
6 青绿 稍蜷 浊响 清晰 稍凹 软粘 0.403 是
7 乌黑 稍蜷 浊响 稍糊 稍凹 软粘 0.481 是
8 乌黑 稍蜷 浊响 清晰 稍凹 硬滑 0.437 是
9 乌黑 稍蜷 沉闷 稍糊 稍凹 硬滑 0.666 否
10 青绿 硬挺 清脆 清晰 平坦 软粘 0.243 否
11 浅白 硬挺 清脆 模糊 平坦 硬滑 0.245 否
12 浅白 蜷缩 浊响 模糊 平坦 软粘 0.343 否
13 青绿 稍蜷 浊响 稍糊 凹陷 硬滑 0.639 否
14 浅白 稍蜷 沉闷 稍糊 凹陷 硬滑 0.657 否
15 乌黑 稍蜷 浊响 清晰 稍凹 软粘 0.36 否
16 浅白 蜷缩 浊响 模糊 平坦 硬滑 0.593 否

由于基于信息增益的决策树算法一般适用于离散属性，若要处理连续属性则必须将其按照一定规则转为离散属性。所以在接下来的代码实现当中我们使用二分法将连续属性离散化。

Python实现过程

1.算法过程

计算信息熵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def calEntropy(dataArr, classArr):
    """
    calculate information entropy.
    :param dataArr:
    :param classArr:
    :return: entropy
    """
    n = dataArr.size
    data0 = dataArr[classArr == 0] #这种用法只对array有效，对list无效
    data1 = dataArr[classArr == 1]
    p0 = data0.size / float(n)
    p1 = data1.size / float(n)
    # 约定：p=0, p*log_2(p) = 0
    if p0 == 0:
        ent = -(p1 * np.log(p1))
    elif p1 == 0:
        ent = -(p0 * np.log(p0))
    else:
        ent = -(p0 * np.log2(p0) + p1 * np.log2(p1))
    return ent
计算信息增益
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def calInfoGain(dataSet, labelList, ax, value=-1):
    """
    计算给定数据dataSet在属性ax上的香农熵增益。

    input：
        dataSet：输入数据集，形状为(m,n)表示m个数据，前n-1列个属性，最后一列为类型。
        labelList：属性列表，如['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度']
        ax: 选择用来计算信息增益的属性。1表示第一个属性，2表示第二个属性等。
                    前六个特征是标称型，后一个特征是数值型。
        value: 用来划分数据的值。当标称型时默认为-1, 即不使用这个参数。

    return：
        gain:信息增益
    """
    baseEnt = calEntropy(dataSet[:, :-1], dataSet[:, -1])  # 计算D的原始信息熵

    newEnt = 0.0  # 划分完数据后的香农熵
    # 离散型
    if ax < dataSet.shape[1] - 2:  # 计算标称型的香农熵
        num = len(featureDic[labelList[ax]])   # 每一个特征的类别数
        for j in range(num):
            subDataSet = splitDataSet(dataSet, ax, j + 1)
            prob = len(subDataSet) / float(len(dataSet))
            if prob != 0:
                newEnt += prob * calEntropy(subDataSet[:, :-1], subDataSet[:, -1])
    # 连续型
    else:
        # 数据集划分为两份
        dataL, dataR = splitDataSet(dataSet, ax, value)
        # 计算两数据集的信息熵
        entL = calEntropy(dataL[:, :-1], dataL[:, -1])
        entR = calEntropy(dataR[:, :-1], dataR[:, -1])
        # 计算划分完总数据集的信息熵
        newEnt = (dataL.size * entL + dataR.size * entR) / float(dataSet.size)

    # 计算信息增益
    gain = baseEnt - newEnt
    return gain
生成树主要代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def createTree(dataSet, labels):
    """
    通过信息增益递归创造一颗决策树。
    input:
        labels
        dataSet

    return:
        myTree: 返回一个存有树的字典
    """
    classList = dataSet[:, -1]
    # 如果剩余的类别全相同,则返回
    if len(classList[classList == classList[0]]) == len(classList):
        if classList[0] == 0:
            return '坏瓜'
        else:
            return '好瓜'
    # 如果只剩下类标签，投票返回
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)

    # 得到增益最大划分的属性、值
    bestFeat, bestVal, entGain = chooseBestSplit(dataSet, labels)
    bestFeatLabel = labels[bestFeat]

    if bestVal != -1:  # 如果是数值型
        txt = bestFeatLabel + "<=" + str(bestVal) + "?"
    else:   # 如果是标称型
        txt = bestFeatLabel + "=" + "?"

    myTree = {txt: {}}  # 创建字典，即树的节点。
    if bestVal != -1:   # 连续型的话就是左右两个子树。
        subDataL, subDataR = splitDataSet(dataSet, bestFeat, bestVal)
        myTree[txt]['是'] = createTree(subDataL, labels)
        myTree[txt]['否'] = createTree(subDataR, labels)
    else:
        i = 0
        # 生成子树的时候要将已遍历的属性删去。连续型不要删除。
        del (labels[bestFeat])
        uniqueVals = featureDic[bestFeatLabel]  # 最好的特征的类别列表
        for value in uniqueVals:    # 标称型的属性值有几种，就要几个子树。
            # Python中列表作为参数类型时，是按照引用传递的，要保证同一节点的子节点能有相同的参数。
            subLabels = labels[:]  # subLabels = 注意要用[:]，不然还是引用
            i += 1
            subDataSet = splitDataSet(dataSet, bestFeat, i)
            myTree[txt][value] = createTree(subDataSet, subLabels)

    return myTree

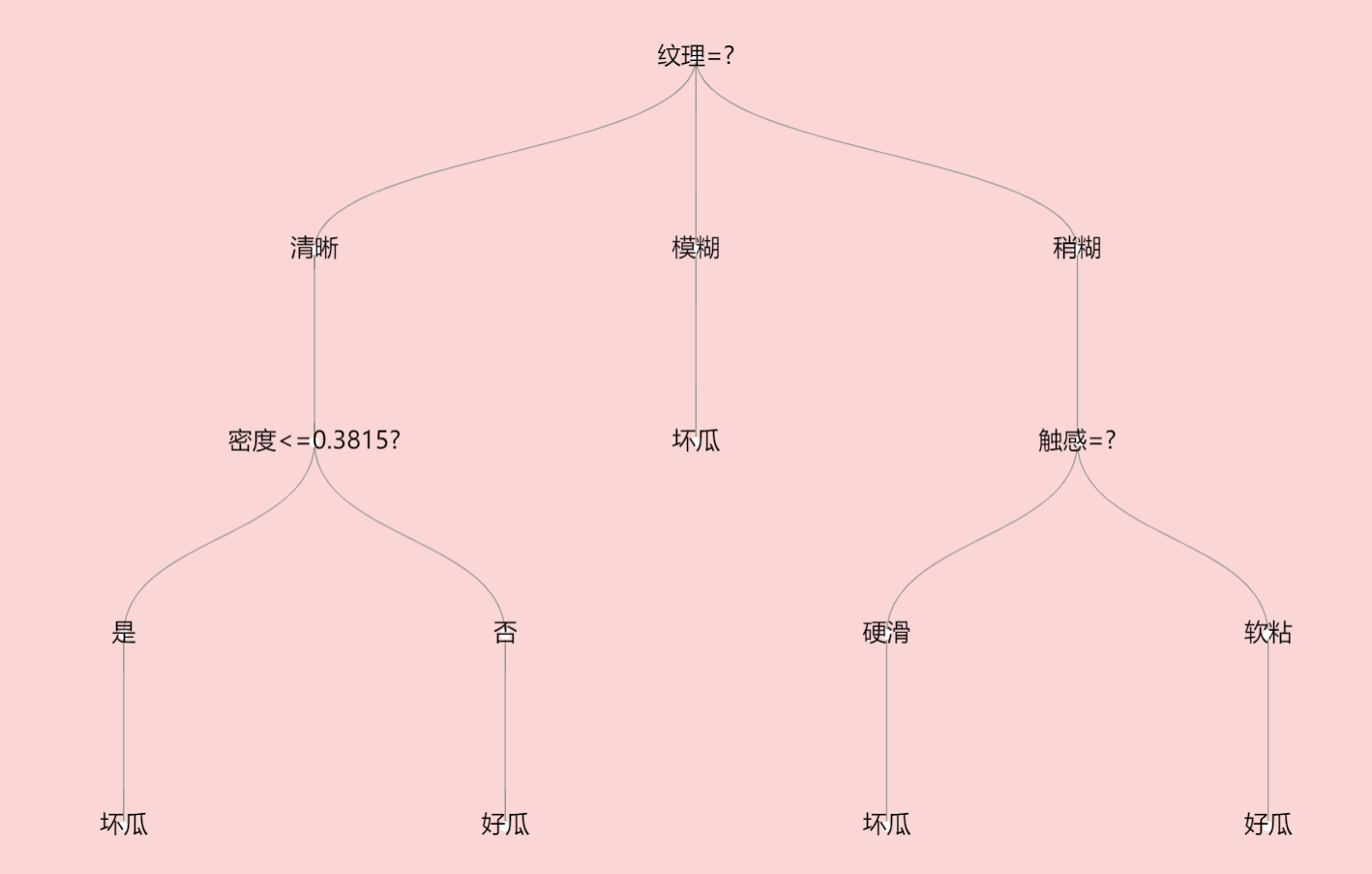
生成树字典为：{‘纹理=?’: {‘清晰’: {‘密度<=0.3815?’: {‘是’: ‘坏瓜’, ‘否’: ‘好瓜’}}, ‘模糊’: ‘坏瓜’, ‘稍糊’: {‘触感=?’: {‘硬滑’: ‘坏瓜’, ‘软粘’: ‘好瓜’}}}}

2.可视化

使用javascript中echart库对生成树进行可视化，通过引入json的方式进行字典的调用。

image-20220322182028236